[FP & LINQ via C# series]#

[Category Theory via C# series]#

Monoid and monoid laws#

Monoid is an important algebraic structure in category theory. A monoid M is a set M equipped with a binary operation ⊙ and a special element I, denoted 3-tuple (M, ⊙, I), where

• M is a set of elements
• ⊙ is a binary operator called multiplication, so that M ⊙ M → M, which means the multiplication of 2 elements in set M always results an element in set M. This operation is also denoted μ, so that μ(M, M) ≡ M ⊙ M.
• I is a special unit element (aka neutral element, or identity element) in set M

And the binary operator and the unit element must satisfy the following monoid laws:

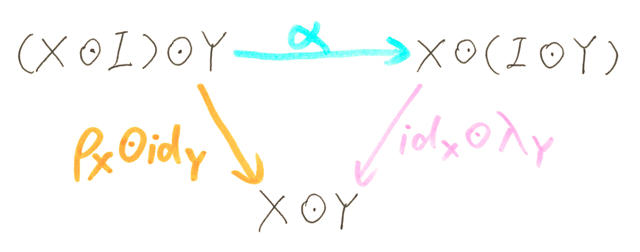
• associative law αX, Y, Z: (X ⊙ Y) ⊙ Z ≡ X ⊙ (Y ⊙ Z), where X ∈ M, Y ∈ M, Z ∈ M
• left unit law λX: I ⊙ X ≡ X, where X ∈ M; and right unit law ρX: X ≡ X ⊙ I, where X ∈ M

so that:

• the triangle identity commutes:
• and the pentagon identity commutes::

In C#, the monoid definition can be represented as:

1
public interface IMonoid<T>
2
{
3
    static abstract T Multiply(T value1, T value2);
4

5
    static abstract T Unit { get; }
6
}

An intuitive example is the set ℤ of all integers, with binary operator + and unit element 0. The addition of 2 integers always results another integer; Also for integers x, y ,z, there is (x + y) + z ≡ x + (y + z) and 0 + x ≡ x ≡ x + 0 (ℤ, +, 0), so that (ℤ, +, 0) is monoid. Apparently (ℤ, *, 1) is monoid too.

1
public class Int32SumMonoid : IMonoid<int>
2
{
3
    public static int Multiply(int value1, int value2) => value1 + value2;
4

5
    public static int Unit => GenericIndirection.AdditiveUnit<int>(); // 0.
6
}
7

8
public class Int32ProductMonoid : IMonoid<int>
9
{
10
    public static int Multiply(int value1, int value2) => value1 * value2;
11

12
    public static int Unit => GenericIndirection.MultiplicativeUnit<int>(); // 1.
13
}
14

15
public static class GenericIndirection
16
{
17
    public static T AdditiveUnit<T>() where T : IAdditiveIdentity<T, T> => T.AdditiveIdentity;
18

19
    public static T MultiplicativeUnit<T>() where T : IMultiplicativeIdentity<T, T> => T.MultiplicativeIdentity;
20
}

Another monoid example is (string, string.Concat, string.Empty):

1
public class StringConcatMonoid : IMonoid<string>
2
{
3
    public static string Multiply(string value1, string value2) => string.Concat(value1, value2);
4

5
    public static string Unit => string.Empty;
6
}

Here string can be viewed as a sequence of char, and the unit string is an empty sequence. Generally, (IEnumerable, Enumerable.Concat, Enumerable.Empty()) is a monoid:

1
public class EnumerableConcatMonoid<T> : IMonoid<IEnumerable<T>>
2
{
3
    public static IEnumerable<T> Multiply(IEnumerable<T> value1, IEnumerable<T> value2) => value1.Concat(value2);
4

5
    public static IEnumerable<T> Unit => Enumerable.Empty<T>();
6
}

The set of Boolean values { true, false }, with binary operator && and unit element true, is a monoid with only 2 element: ({true, false}, &&, true); And so is ({ true, false }, ||, false):

1
public class BooleanAndMonoid : IMonoid<bool>
2
{
3
    public static bool Multiply(bool value1, bool value2) => value1 && value2;
4

5
    public static bool Unit => true;
6
}
7

8
public class BooleanOrMonoid : IMonoid<bool>
9
{
10
    public static bool Multiply(bool value1, bool value2) => value1 || value2;
11

12
    public static bool Unit => false;
13
}

A monoid with 1 single element can be defined with the special type void (System.Void):

1
namespace System
2
{
3
    [ComVisible(true)]
4
    [Serializable]
5
    [StructLayout(LayoutKind.Sequential, Size = 1)]
6
    public struct Void
7
    {
8
    }
9
}

The set { default(void) } with the following operator and unit is a monoid:

1
public class VoidMonoid : IMonoid<void>
2
{
3
    public void Multiply(void value1, void value2) => default;
4

5
    public void Unit() => default;
6
}

However, C# compiler does not allow void keyword or System.Void type to be used in this way, so here System.Void can be replaced with its equivalency in F#, the Microsoft.FSharp.Core.Unit type:

1
namespace Microsoft.FSharp.Core
2
{
3
    [CompilationMapping(SourceConstructFlags.ObjectType)]
4
    [Serializable]
5
    public sealed class Unit : IComparable
6
    {
7
        internal Unit() { }
8

9
        public override int GetHashCode() => 0;
10

11
        public override bool Equals(object obj) =>
12
            obj == null || LanguagePrimitives.IntrinsicFunctions.TypeTestGeneric<Unit>(obj);
13

14
        int IComparable.CompareTo(object obj) => 0;
15
    }
16
}

With an internal constructor, Unit cannot be instantiated, a Unit variable can only be default(Unit), which is null. So similarly, set { default(Unit) } with the following operator and unit element is monoid:

1
public class UnitMonoid : IMonoid<Unit>
2
{
3
    public static Unit Multiply(Unit value1, Unit value2) => default;
4

5
    public static Unit Unit => default;
6
}

Monoid as category#

An individual monoid (M, ⊙, I) can be a category C with 1 single object M, where:

• The collection of objects ob(C) is { M }, which means, category C has 1 single object, that is M.
• The collection of orphisms hom(C) is set M itself, which mean, each elements in set M is a morphism in category C.
• The composition operation ∘ of C is ⊙: since each morphism in C is each element in M, the composition of morphisms is just the multiplication of elements.
• The identity morphism id of C is unit element I: the identity morphism in C is the unit element in M

In this way, since M, ⊙, I satisfies the monoid laws, apparently the category laws are satisfied. In C#, this singleton category can be represented as:

1
public class MonoidCategory<T, TMonoid> : ICategory<Type, T> where TMonoid : IMonoid<T>
2
{
3
    public static IEnumerable<Type> Objects { get { yield return typeof(TMonoid); } }
4

5
    public static T Compose(T morphism2, T morphism1) => TMonoid.Multiply(morphism1, morphism2);
6

7
    public static T Id(Type @object) => TMonoid.Unit;
8
}